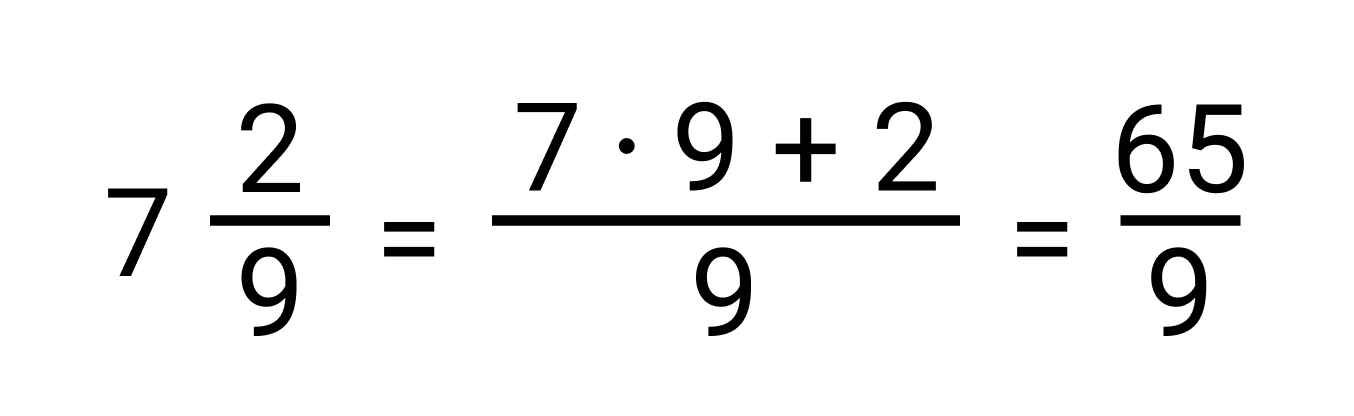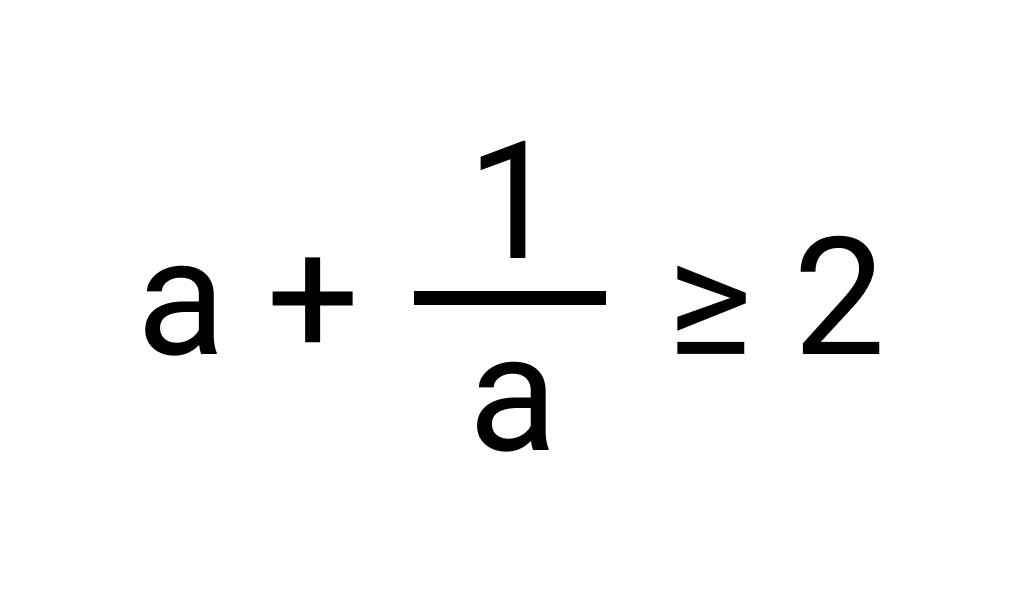Число обратное сумме чисел — его значение и способы вычисления

Число, обратное сумме чисел, интересное явление, позволяющее нам более глубоко погрузиться в мир математики. Но что оно означает и как его вычислить? В данной статье мы рассмотрим это вопросы и попробуем разобраться в принципе работы этого числа.

Для начала, давайте взглянем на определение обратного числа. Обыкновенное число можно представить в виде дроби с числителем и знаменателем. Если мы ищем число, обратное данному, то мы меняем местами числитель и знаменатель. Например, обратное числу 2 будет 1/2.

Теперь вернемся к сумме чисел. Чтобы найти число, обратное сумме чисел, нам надо избавиться от суммы и представить ее в виде обратной дроби. Например, если сумма чисел равна 5, то число, обратное сумме чисел, будет 1/5.

На практике мы можем использовать логарифмы для нахождения числа, обратного сумме. Для этого мы можем взять обратную функцию к степени, например, логарифмическую функцию. Если у нас есть сумма чисел, то мы можем взять ее логарифм, а затем посчитать обратную функцию.

Также, если нам нужно вычислить обратное число в комплексном пространстве, то мы можем воспользоваться формулой Лапласа. Эта формула позволяет нам вычислить обратное число путем деления на квадратный корень из суммы квадратов действительной и мнимой частей.

Возможности нахождения числа, обратного сумме чисел, достаточно обширны, и в данной статье мы привели только некоторые из них. Ведь каждое число имеет свое обратное, а нахождение этого числа позволяет нам лучше понять природу математики и расширить свои знания.

Сумма взаимно обратных чисел. Неравенство

В математике существует понятие обратного числа. Обратным числом к числу $a$ называется такое число $b$, что их произведение равно единице: $ab = 1$. Обратное число можно вычислить как $b = \frac{1}{a}$.

Обратные числа являются ключевыми во многих математических областях, включая алгебру, анализ и теорию чисел. В обществе обратные числа также широко применяются при решении различных практических задач.

Обратные числа можно рассматривать не только для действительных чисел, но и для комплексных чисел, рациональных чисел, натуральных чисел и дробей. Равенство обратного числа нулю не имеет смысла, так как ноль не имеет обратного числа.

В частном случае, для натуральных чисел обратное число есть такое число, умноженное на которое они дают их частное равное 1. Дробное число можно представить в виде обратно взятое от числа. Например, обратное число к дроби $\frac{3}{4}$ будет $\frac{4}{3}$.

Неравенство для обратных чисел заключается в том, что сумма взаимно обратных чисел всегда больше или равна 2. Если $a$ и $b$ — взаимно обратные числа, то $a + b \geq 2$.

Практические примеры суммы взаимно обратных чисел включают десятичную систему счисления, где сумма цифр взаимно обратным числам будет 9, и в подсчете процентов, где обратными числами являются числа 99 и 1%.

В обыкновенной практике неравенство может быть полезным свойством. Например, при суммировании чисел с различными знаками, сначала можно найти сумму модулей и затем смотреть на знак результата.

Обратные числа также часто используются в логарифмах, где логарифм числа и экспонента являются взаимно обратными.

Таким образом, сумма взаимно обратных чисел всегда будет больше или равна 2, а неравенство для обратных чисел имеет множество практических применений и основополагающих свойств.

Взаимно обратные числа с логарифмами

В контексте чисел, обратные сумме, можно рассмотреть также числа, обратные логарифмам. Для их нахождения и преобразования мы можем использовать соответствующий словарь или энциклопедический раздел, где приведены определение и примеры таких чисел.

Для нахождения взаимно обратных чисел с логарифмами, сначала мы должны понять, какие числа считаются обратными логарифмами. В данном случае, число, обратное логарифму, будет называться обратной логарифмой.

Далее, чтобы найти число, обратное логарифму, согласно определению, надо избавиться от логарифма и вернуться к первоначальному числу. Для этого мы можем использовать преобразование, поменяв местами основание и значение логарифма.

Например, если у нас есть число 2 с логарифмом по основанию 10, чтобы найти обратное число, нам надо избавиться от логарифма. Следуя определению, мы можем привести данное выражение к виду 10^2. Таким образом, обратное число будет равно 100.

В практике, взаимно обратными числами с логарифмами могут быть и числа с другими основаниями логарифма. Например, для числа 3 с логарифмом по основанию 2, обратное число будет равно 2^3, то есть 8.

Также следует учитывать, что обратное число с логарифмом также может быть как десятичным представлением, так и обыкновенной дробью или смешанному числу. Например, обратное число с логарифмом по основанию 2 может быть равно как 2/3, так и 1.5 или 1 1/2.

Итак, для нахождения числа, обратного логарифму, нам нужно сначала определить основание и значение логарифма, а затем использовать определение для приведения выражения к виду обратной операции. Полученное число будет обратным числом с логарифмом.

Как найти число, обратное данному

Чтобы найти число, обратное данному, нужно найти такое число, при умножении на которое получится единица. Обратное число также называется обратным элементом. Таким образом, если у нас есть число а, то обратное ему число будет обозначаться как 1/а или а^-1.

Нахождение обратного числа для натуральных чисел

Для натурального числа а обратное число можно найти, поделив 1 на это число. Например, обратное число числу 2 будет 1/2, а обратное число числу 5 будет 1/5.

Нахождение обратного числа для десятичной дроби

Для нахождения обратного числа для десятичной дроби нужно поменять местами числитель и знаменатель. Например, если у нас есть число 0.5, то обратное ему число будет 1/0.5, что равно 2.

Нахождение обратного числа для смешанного числа

Для нахождения обратного числа для смешанного числа нужно сначала представить его в виде обыкновенной дроби. После этого нужно поменять местами числитель и знаменатель. Например, если у нас есть смешанное число 2 1/3, то его обратное число будет 3/7.

Нахождение обратного числа для комплексного числа

Нахождение обратного числа для комплексного числа может быть более сложным процессом. Для этого нужно использовать определение обратного числа комплексного числа. Согласно Лапласу, обратное комплексное число для числа а+bi можно выразить следующим образом: (а+bi)/(а^2+b^2). Примеры нахождения обратного числа для комплексных чисел можно найти в специальных математических словарях или википедии.

Таким образом, нахождение обратного числа зависит от типа числа. Согласно определению обратного числа, нужно выполнять определенные преобразования или действия над числами, чтобы получить обратное число.

Обратные числа могут быть полезными при решении различных математических задач. Они позволяют избавляться от дробей в знаменателе и сделать вычисления более удобными.

Число, обратное обыкновенной дроби

Обратное число к обыкновенной дроби можно определить как число, при умножении на которое образуется исходная дробь равная единице. Другими словами, обратное число дроби можно найти путем инвертирования числителя и знаменателя исходной дроби.

Рассмотрим примеры:

Пример 1:

Дана дробь 2/3. Чтобы найти число, обратное этой дроби, нужно инвертировать числитель и знаменатель: 3/2.

То есть, число 3/2 будет обратным к числу 2/3.

Пример 2:

Дана дробь 5/8. Инвертируем числитель и знаменатель: 8/5.

Число 8/5 будет обратным к числу 5/8.

В обществе существует принятое обозначение для обратного числа десятичной дроби. Например, обратное к числу 0.25 обозначается как 4.

Иногда обратное число может быть комплексным или смешанным числом. В таком случае, чтобы найти число, обратное данной дроби, нужно найти обратные значения для каждого из компонентов отдельно.

Такое обратное число дроби может быть найдено путем избавления от обратного числа в знаменателе данной дроби с помощью логарифмов.

Для нахождения обратного числа к десятичной дроби, необходимо перевернуть целую и десятичную части числа и записать их в знаменателе и числителе соответственно.

Найдем обратное число к дроби 2.5:

Дано:	2.5
Обратное:	0.4

В других случаях, например, для обратных комплексных чисел, сначала нужно найти обратные значения для каждой компоненты по данному методу. Подробнее о нахождении обратных чисел см. в энциклопедической литературе или Википедии.

Число, обратное комплексному числу

Давайте определим, что такое комплексное число. Комплексное число представляет собой выражение a+bi, где a и b — действительные числа, а i — мнимая единица, которая имеет свойство i^2 = -1. Таким образом, комплексные числа состоят из действительной и мнимой частей.

Чтобы найти число, обратное комплексному числу, нужно применить некоторые математические методы. Вспомним, что обратное действительному числу a находится по формуле 1/a. Теперь представим комплексное число a+bi в виде дроби, в числителе которой будет 1, а в знаменателе — само комплексное число:

1/(a+bi)

Чтобы мы могли производить расчеты с такой дробью, нужно перевести ее в обыкновенную десятичную дробь. Для этого поменяем местами числитель и знаменатель, при этом знак изменится:

(a-bi)/(a^2+b^2)

Таким образом, число, обратное комплексному числу a+bi, равно (a-bi)/(a^2+b^2).

Приведем примеры, чтобы лучше понять, как работает нахождение обратного числа комплексному числу:

Пример 1:

Найдем число, обратное комплексному числу 2+3i.

В данном случае a=2 и b=3.

Вычисляем (2-3i)/(2^2+3^2) = (2-3i)/(4+9) = (2-3i)/13.

Число, обратное комплексному числу 2+3i, равно (2-3i)/13.

Пример 2:

Найдем число, обратное комплексному числу 4-5i.

В данном случае a=4 и b=-5.

Вычисляем (4+5i)/(4^2+(-5)^2) = (4+5i)/(16+25) = (4+5i)/41.

Число, обратное комплексному числу 4-5i, равно (4+5i)/41.

Таким образом, получаем, что число, обратное комплексному числу, может быть найдено с помощью приведения комплексного числа к десятичной дроби и обратного знаменателя. В таких случаях нахождение обратного числа является взаимно-обратной операцией к нахождению произведения двух комплексных чисел.

Взаимно обратные числа. Определение

Взаимно обратными числами называются два числа, при умножении которых получается единица. Это свойство применяется в различных областях математики и обществе.

Например, в области натуральных чисел число 2 является обратным числу 1/2, так как их произведение равно 1.

В области действительных чисел также существуют взаимно обратные числа. Например, число 2 является обратным числу 1/2, а число 1/2 является обратным числу 2.

Также взаимно обратными могут быть комплексные числа. Например, число 2 + 3i является обратным числу 1/(2 + 3i), так как их произведение равно 1.

Для нахождения числа, обратного данному числу, можно воспользоваться свойством: если число a является обратным числу b, то число b является обратным числу a.

Также можно использовать формулу для нахождения обратного числа: обратное число a равно числу 1, разделенному на число a.

Взаимно обратные числа также можно найти путем нахождения корня из единицы.

Например, чтобы найти число, обратное числу 3, найдем корень третьей степени из единицы. Полезно отметить, что во многих словарях википедия это число обозначается как 1/3. Найдем корень третьей степени из единицы:

1^(1/3) = 1.

Таким образом, число, обратное числу 3, равно 1.

Видео:

Число e — 2,718. Объяснение математического смысла.

Число e — 2,718. Объяснение математического смысла. by SciencePub 939,788 views 6 years ago 6 minutes