Узнайте, почему шаблонные параболы необходимы для успешного использования и как правильно применять их!

Шаблонная парабола является одним из основных инструментов исследовательской работы в математике. Построение графика квадратичной функции позволяет лучше изучить ее особенности и свойства. Коэффициенты квадратичной функции в уравнении y = ax^2 + bx + c влияют на форму и направление параболы. Используя шаблонную параболу, эксперты и студенты могут более точно изучить функцию и построить график.

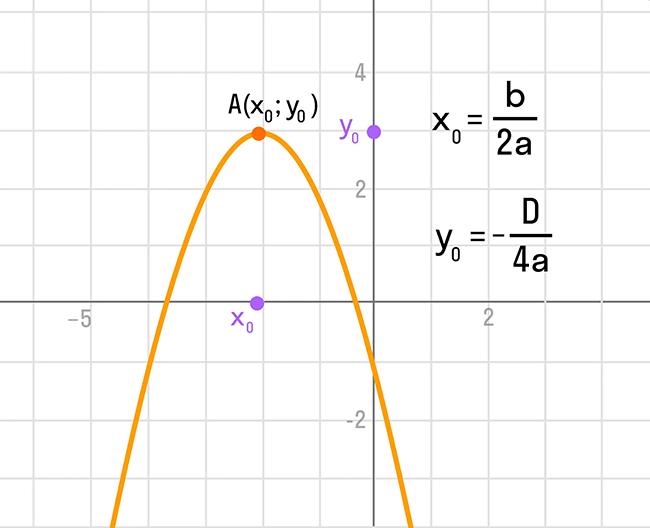
Основные ветви параболы пересекаются в точке с координатами (x₀, y₀), которая называется вершиной параболы. Зная координаты вершины и направление параболы, можно определить момент, когда график функции пересекает ось Ox и когда достигается минимальное или максимальное значение функции.

Важной частью построения графика является определение коэффициентов a, b и c в уравнении параболы. Исследуя значения коэффициентов, можно понять, как они влияют на вид и форму параболы, а также ее положение на графике. Например, коэффициент a определяет, насколько быстро парабола расширяется вдоль оси Ox, а коэффициент c задает сдвиг графика вверх или вниз.

Ход урока

Начинаем с презентации материала о квадратичной функции и ее графике — параболе. Рассмотрим уравнение параболы вида y = ax² + bx + c и определим основные понятия: коэффициенты a, b, c, вершина параболы, симметричность ее ветвей относительно вертикальной прямой, смещение вдоль оси oy вверх или вниз. Все полученные знания будут нужны нам в дальнейшем исследовании работы параболы.

В группе экспертов выбирается старший ученик, который будет отвечать на вопросы и помогать другим ученикам во время урока. Мы начинаем исследование функции путем построения графиков параболы при различных значениях коэффициентов a, b, c. Построение графика начинаем с функции вида y = ax².

В этот момент определим смещение графика параболы. Для этого подставим в уравнение функции параболы b = 0 и анализируем полученные значения функции в зависимости от направления смещения (вверх или вниз) и величины сдвига. Результаты запишем в таблицу.

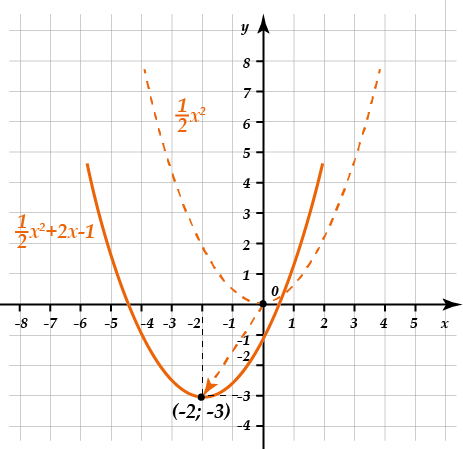
Далее рассмотрим функцию y = ax² + b. Здесь коэффициент b отвечает за смещение параболы вдоль оси oy. Мы изучим, как изменяется график параболы при различных значениях коэффициента b. Зафиксируем значение коэффициента a и будем сдвигать параболу по вертикали, изменяя значение b. Запишем результаты в таблицу и проанализируем изменения графика.

Последним шагом будем изучать параболу вида y = ax² + bx + c. Здесь коэффициент c определяет положение параболы относительно оси Ox — смещение графика вдоль оси Ox влево или вправо. Построим график параболы при разных значениях коэффициента c, записав результаты в таблицу. Анализируя полученные значения, ученики смогут улучшить понимание смещения графика вдоль оси Ox.

Уравнение квадратичной функции имеет вид y = ax² + bx + c

Для построения графика квадратичной функции можно использовать шаблонную параболу, которая помогает представить общий облик графика и определить основные характеристики функции.

Организационный аспект

• Определить значения коэффициентов a, b и c в уравнении квадратичной функции.
• Найти значения абсцисс (x-координат) точек на графике функции.
• Подставить значения абсцисс в уравнение функции для определения соответствующих ординат (y-координат).
• Построить полученные точки на графике.
• Определить дополнительные характеристики функции, такие как направление ветвей параболы, точка пересечения с осью ординат (y-осью) и показатели роста и убывания функции.

Алгоритм построения графика

1. Определить значения коэффициентов a, b и c в уравнении квадратичной функции.
2. Найти значения абсцисс точек на графике функции.
3. Подставить значения абсцисс в уравнение функции для определения соответствующих ординат.
4. Построить полученные точки на графике.
5. Определить дополнительные характеристики функции.

Попробуем применить полученные знания на практике:

Пример

Рассмотрим уравнение квадратичной функции y = x².

Для построения графика функции, определим значения абсцисс и ординат на основе уравнения:

• Подставим x = -2: y = (-2)² = 4.
• Подставим x = -1: y = (-1)² = 1.
• Подставим x = 0: y = 0² = 0.
• Подставим x = 1: y = 1² = 1.
• Подставим x = 2: y = 2² = 4.

Полученные значения точек (x, y) на графике функции: (-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4).

Теперь построим график функции, используя полученные точки:

В результате получим график параболы с вершиной в точке (0, 0) и симметричной относительно оси ординат. Дополнительно можно определить направление ветвей параболы и точку пересечения с осью абсцисс.

Таким образом, шаблонная парабола позволяет наглядно представить и анализировать графики квадратичных функций, а использование уравнения квадратичной функции позволяет определить точки на графике и рассчитать дополнительные характеристики функции.

Уравнение квадратичной функции имеет вид y = x² + a · x + b

В данной статье мы рассмотрим алгоритм построения графика квадратичной функции, которая имеет вид y = x² + a · x + b.

Шаг 1: Определите значения коэффициентов a, b и c в уравнении. Коэффициент a отвечает за коэффициент при x², коэффициент b — за коэффициент при x, и коэффициент c — за свободный член.

Шаг 2: Определите дискриминант по формуле D = b² — 4ac. Дискриминант позволяет определить, сколько решений имеет уравнение и какие они.

Шаг 3: Рассмотрим случаи в зависимости от значения дискриминанта:

3.1. Дискриминант больше нуля: если D > 0, то уравнение имеет два различных корня. График функции будет состоять из двух ветвей, которые будут открыты вниз, а точки пересечения с осью абсцисс будут корнями уравнения.

3.2. Дискриминант равен нулю: если D = 0, то уравнение имеет один корень. График функции будет представлять собой вершину параболы, которая будет касаться оси абсцисс в этой точке.

3.3. Дискриминант меньше нуля: если D < 0, то уравнение не имеет действительных корней. График функции будет представлять собой параболу, которая не пересекает ось абсцисс.

Таким образом, в зависимости от значения дискриминанта, график функции будет иметь различные характеристики. При помощи построения и анализа данного графика можно получить важную информацию о поведении функции в различных точках.

В конечном итоге, изучение и использование уравнения квадратичной функции y = x² + a · x + b является важным инструментом для множества областей работы и исследования, таких как математика, физика, экономика и другие.

Построение квадратичной функции

На уроке материала учащимся предлагается провести исследовательскую работу для закрепления основных понятий квадратичной функции. Учащиеся работают в группе, и момент рефлексии происходит на этапе рассмотрения полученных результатов.

Для построения графика квадратичной функции мы должны знать значение коэффициентов a, b и c. С помощью этих значений учащиеся могут составить уравнение функции и подставить различные значения переменной x, чтобы получить соответствующие точки графика.

Ошибки при построении графика квадратичной функции могут возникнуть, если применены неправильные значения коэффициентов a, b и c или если неправильно подобраны точки для построения графика.

Например, если коэффициент a равен нулю, то уравнение функции становится линейным, а график будет прямой линией, которая не имеет параболической формы. Если коэффициенты b и c равны нулю, то график функции будет проходить через начало координат (0, 0).

Кроме того, график квадратичной функции может быть сдвинут вверх или вниз или вправо или влево относительно оси x в соответствии с значениями коэффициентов b и c.

Рассмотрим пример: y = -2x² + 3x + 1. В данном уравнении коэффициенты a, b и c равны -2, 3 и 1 соответственно. Используя эти значения, учащиеся могут построить график функции, подставляя различные значения переменной x и находя соответствующие значения y.

На слайде №11 урока подставим значения x от -5 до 5 и получим соответствующие значения y, по которым можно построить график функции.

Момент рефлексии на уроке включает в себя обсуждение полученных результатов и определение, как значения коэффициентов a, b и c влияют на форму графика квадратичной функции.

• Коэффициент a отвечает за степень «уклона» параболы. Если a положительное число, то парабола открывается вверх, а если отрицательное, то вниз.
• Коэффициент b определяет смещение функции по горизонтали. Чем больше b, тем больше смещение функции вправо, а чем меньше b, тем больше смещение функции влево.
• Коэффициент c влияет на вертикальное смещение функции. Если c положительное число, то функция смещается вверх, а если отрицательное, то вниз.

Итак, построение графика квадратичной функции включает в себя рефлексию полученных результатов, исследование влияния коэффициентов a, b и c на форму графика и закрепление основных концепций квадратичной функции.

Исследовательская работа

Для лучшего понимания принципов построения и использования шаблонной параболы, проведем исследовательскую работу.

Алгоритм действий определим следующим образом:

1. В начале урока проведем краткую презентацию о понятиях параболы, уравнения функции и основных коэффициентов, которые влияют на ее вид и положение.
2. Для закрепления знаний в организационной группе проведем упражнение, в ходе которого будем строить параболу по заданным коэффициентам, а также уравнению квадратичной функции y = ax^2 + bx + c.
3. С помощью полученных результатов построим график параболы функции y = ax^2 + bx + c и определим основные характеристики этой функции:

   — Направление открытия ветвей параболы (вверх или вниз);

   — Координаты вершины параболы;

   — Точки пересечения параболы с осями абсцисс и ординат;

   — Значение коэффициентов a, b и c в уравнении функции.

4. По полученным данным определим, какие значения коэффициентов a, b и c в уравнении ax^2 + bx + c приводят к изменению формы и положения параболы, а также координат вершины и направления открытия ветвей.
5. На основе полученных результатов составим статью, где представим график и основные характеристики функции в соответствии с уравнением y = ax^2 + bx + c. Кроме того, мы рассмотрим примеры парабол, где будут использованы единичные коэффициенты и коэффициенты, сдвинутые по оси абсцисс и ординат.

В итоге исследовательской работы мы получим глубокое понимание характеристик параболы, алгоритма ее построения и использования в различных контекстах. Также мы будем знать, какие ошибки могут возникнуть при построении параболы на основе предоставленного материала, и как их избежать.

Квадратичная функция. Построение параболы

Для построения графика параболы с помощью шаблонной параболы можно использовать следующий алгоритм:

1. Определить координаты вершины параболы. Для этого нужно найти координаты вершины (-b/(2a), f(-b/(2a))).
2. Определить направление открытия параболы. Если коэффициент a > 0, то парабола будет направлена вверх, если a < 0, то вниз.
3. Найти дискриминант D = b^2 — 4ac. Если D > 0, то парабола пересекает ось абсцисс в двух точках, если D = 0, то в одной точке, если D < 0, то не пересекает.
4. Построить график параболы с учетом найденных результатов. Для этого можно использовать точки (x, f(x)), где x — значения из определенного интервала вокруг вершины параболы.

Рассмотрим пример построения параболы по уравнению f(x) = 2x^2 — 3x + 1.

Шаг 1: Определение вершины параболы

Для функции f(x) = 2x^2 — 3x + 1 коэффициент a = 2, b = -3, c = 1. Подставим эти значения в формулу для координат вершины:

a	b	c
2	-3	1

Таким образом, координаты вершины параболы будут (-(-3)/(2*2), f(-(-3)/(2*2))) = (3/4, f(3/4)).

Шаг 2: Определение направления параболы

Так как коэффициент a = 2 > 0, парабола будет направлена вверх.

Шаг 3: Определение дискриминанта

Для функции f(x) = 2x^2 — 3x + 1 коэффициенты a = 2, b = -3, c = 1. Подставим их в формулу для дискриминанта: D = -3^2 — 4*2*1.

a	b	c	D
2	-3	1	1

Таким образом, дискриминант равен D = 1.

Шаг 4: Построение графика параболы

Используя найденные результаты, построим график параболы:

— Найдем значения функции f(x) для нескольких значений x в окрестности вершины параболы.

— Отметим точку вершины параболы (3/4, f(3/4)).

— Соединим найденные точки, чтобы построить параболу.

Таким образом, построение параболы по уравнению f(x) = 2x^2 — 3x + 1 завершено.

В результате выполнения данной работы ученик изучит материал о квадратичной функции и научится строить параболу по ее уравнению. Это позволит закрепить основные понятия, изученные на уроке, а также развить исследовательскую работу и работу в группе.

Для организационного хода урока можно использовать слайд с примером построения шаблонной параболы, например №11. Слайд может содержать уравнение параболы, а также необходимые комментарии и указания.

Исследования экспертов показывают, что работа с шаблонной параболой положительно влияет на результаты изучения материала о квадратичной функции. Она помогает ученикам лучше понять понятия абсцисс точек, коэффициентов при x^2 и x в уравнении параболы, а также форму графика квадратичной функции.

Основные понятия

Для успешного проведения урока по построению шаблонной параболы необходимо иметь общее представление о некоторых основных понятиях. Рассмотрим их подробнее:

1. Уравнение квадратичной функции.

   Для построения шаблонной параболы необходимо знать уравнение функции вида y = ax^2 + bx + c, где a, b и c — коэффициенты функции.

2. Сдвиг параболы.

   Сдвиг параболы вдоль оси x происходит при изменении коэффициента a. Если a > 0, парабола сдвигается вверх; если a < 0, парабола сдвигается вниз.

3. Построение шаблонной параболы.

   Для построения шаблонной параболы необходимо определить координаты нескольких точек на параболе. Для этого можно использовать алгоритм, рассмотренный в материале урока.

4. Влияние коэффициентов на вид параболы.

   Изменение коэффициентов a, b и c в уравнении параболы влияет на ее форму и положение. Необходимо изучить, как изменение каждого из этих коэффициентов влияет на график параболы.

5. Результаты исследования.

   В ходе работы с шаблонной параболой можно получить различные результаты исследования: координаты вершины параболы, ось симметрии, точки пересечения с осями координат и т.д. Необходимо научиться анализировать и интерпретировать полученные результаты.

6. Организационный момент.

   Перед началом урока необходимо организовать группу учащихся и объяснить им цели урока, задачи и материал, который будет изучаться.

7. Рефлексия и закрепление материала.

   По завершению урока необходимо провести рефлексию и обсудить с учащимися полученные результаты, а также закрепить изученный материал.

Каждое из этих понятий играет важную роль в изучении построения шаблонной параболы и позволяет более глубоко понять ее структуру и свойства.

Итог урока слайд №11

Организационный момент

На начало урока каждому ученику были выданы листы с заданиями по теме квадратных функций. Были объявлены цели и задачи урока, а также предполагаемые результаты работы.

Рефлексия урока

Презентация к уроку

Ход работы:

1. Начнем с определения коэффициентов a, b и c в уравнении параболы. Коэффициент a отвечает за направление и открытость параболы, коэффициенты b и c описывают смещение параболы по горизонтали и вертикали соответственно.
2. Определим дискриминант D по формуле D = b² — 4ac. Затем проверим его значение:
   • Если D > 0, то парабола имеет две различные корня и пересекает ось x в двух точках.
   • Если D = 0, то парабола имеет один корень и касается оси x в этой точке.
   • Если D < 0, то парабола не пересекает ось x и не имеет вещественных корней.
3. Построим координатную плоскость и отметим ось x и ось y.
4. Найдем вершину параболы, используя формулу x₀ = -b / (2a) и подставим полученное значение в уравнение параболы, чтобы найти соответствующую точку (x₀, y₀).
5. Далее определим точку пересечения параболы с осью y, это будет точка (0, c).
6. Для закрепления материала продолжим строить несколько точек, подставляя различные значения x в уравнение параболы, и получим соответствующие значения y.
7. Построим полученные точки на графике и соединим их гладкой линией, получив тем самым график квадратичной функции.
8. Завершим работу рефлексией, обсудим результаты и ошибки, которые могли возникнуть в процессе работы.

В результате проведенного исследования мы ознакомились с алгоритмом построения графика параболы и узнали основные характеристики такого графика. Теперь мы можем успешно применить полученные знания при решении задач и анализе квадратичных функций.

Уравнение квадратичной функции имеет вид y = ax² + bx + c

Для понимания функции и построения графика необходимо определить значения коэффициентов a, b и c. Коэффициент a определяет направление открытия параболы и влияет на ее ширину. Коэффициент b влияет на сдвиг параболы по оси x, а коэффициент c определяет смещение параболы по оси y.

Для построения графика квадратичной функции, сначала нужно найти координаты вершины параболы, используя формулы x₀ = -b/2a и y₀ = c — b²/4a. Затем строим параболу, откладывая единичные отрезки по оси x и вычисляя соответствующие значения функции y.

При изучении материала и проведении исследований по теме квадратной функции, концепции параболы и ее свойств могут быть проиллюстрированы с помощью шаблонных парабол. Эти шаблоны представляют собой графики квадратичной функции с различными значениями коэффициентов a, b и c.

В организационном смысле, шаблонные параболы могут быть использованы для закрепления изученного материала. Ученики могут построить графики квадратичных функций, подставив различные значения коэффициентов a, b и c, и анализировать результаты полученных графиков.

Также шаблонная парабола может быть использована в презентации или на слайде, чтобы демонстрировать основные понятия квадратичной функции и ее влияние на график. С помощью шаблонной параболы можно иллюстрировать, как изменение коэффициентов a, b и c влияет на форму и положение параболы.

Алгоритм построения шаблонной параболы:

1. Определить значения коэффициентов a, b и c.
2. Вычислить координаты вершины параболы, используя формулы x₀ = -b/2a и y₀ = c — b²/4a.
3. Построить координатную плоскость и задать масштаб.
4. Отметить на оси абсцисс значение x₀.
5. Откладывать от x₀ влево и вправо единичные отрезки и вычислять соответствующие значения функции y.
6. Провести график параболы, соединив найденные точки.
7. Анализировать полученный график и его свойства.

Таким образом, шаблонная парабола является полезным инструментом для изучения и понимания квадратичной функции. Она помогает визуализировать основные концепции и свойства параболы, а также исследовать результаты изменения коэффициентов a, b и c в уравнении квадратичной функции.

Закрепление изученного материала

1. Построение шаблонной параболы

Для построения шаблонной параболы в формате y = ax^2 + bx + c, необходимо знать значения старшего коэффициента a, коэффициента при переменной b и свободного члена c. В зависимости от полученных результатов, можно определить форму и направление параболы.

2. Исследование уравнения параболы

Исследовательская работа заключается в построении графика параболы и определении её характеристик и свойств. При рассмотрении параболы можно определить вершину параболы, ось симметрии, направление открытия ветвей параболы, а также имеет ли парабола точки пересечения с осями координат.

3. Полученные результаты и рефлексия

Таким образом, закрепление изученного материала в уроке №11 осуществлялось путем построения шаблонной параболы, исследования ее уравнения и получения результатов. Работа с шаблонной параболой позволяет учащимся лучше понять и запомнить основные характеристики параболы и методику ее построения.

Видео:

Повестки раздали таксистам в аэропорту. Навальный пропал. Роскомнадзор вступился за «Слово пацана»

Повестки раздали таксистам в аэропорту. Навальный пропал. Роскомнадзор вступился за «Слово пацана» by Телеканал Дождь 129,188 views Streamed 2 hours ago 30 minutes