Что означает целая доля — определение и примеры — понимание базовых понятий и их применение в реальной жизни

Целая доля – это математическое понятие, которое встречается в различных сферах нашей жизни. Само название уже говорит о том, что эта доля означает целое число или количество чего-либо, разделенное на равные части или доли.

История дробей уходит в древность: египтяне уже в 2-м тысячелетии до н.э. умели проводить операции с дробями. В их трудах можно найти запись дроби в виде частей, разделенных чертой. Например, чтобы обозначить третью часть, они писали число и через слэш цифру, обозначающую знаменатель, – 1/3.

Примеры целых долей встречаются во многих ситуациях. Например, когда мы делим расстояние на равные части, получается доля. Если у нас есть 10 апельсинов и мы решили разделить их на 2 равные части, каждая часть будет представлять собой половину от всех апельсинов, то есть целую долю.

Числа, обозначающие целые доли, называются дробными числами. Как правило, они записываются в виде десятичной дроби или с помощью обыкновенной дроби с числителем и знаменателем. Например, число 0.5 будет обозначать половину, а число 1/4 будет обозначать четвертую долю.

В математических тестах и заданиях регулярно встречаются вопросы, связанные с целыми долями. Дополнительная информация о них может понадобиться, чтобы правильно решить задачу или выполнить тест. Важно знать, что в сравнении с целыми числами, доли могут быть меньше или больше, могут быть одинаковые или разные.

Обыкновенные дроби

Обыкновенная дробь — это число, которое записывается в виде общего дроби. Обычно наша десятичная система счисления не работает для дробей. Но если число можно представить в виде десятичной дроби, то есть она будет равная сумме целой части и десятичной дроби после запятой.

Представим, что мы считали число яблок и у нас оказалось 3 яблока. Значит, мы взяли целое число. Но если мы разделили одно яблоко на 4 равные части, то у нас появились дроби. Четверть яблока — это уже дробная часть.

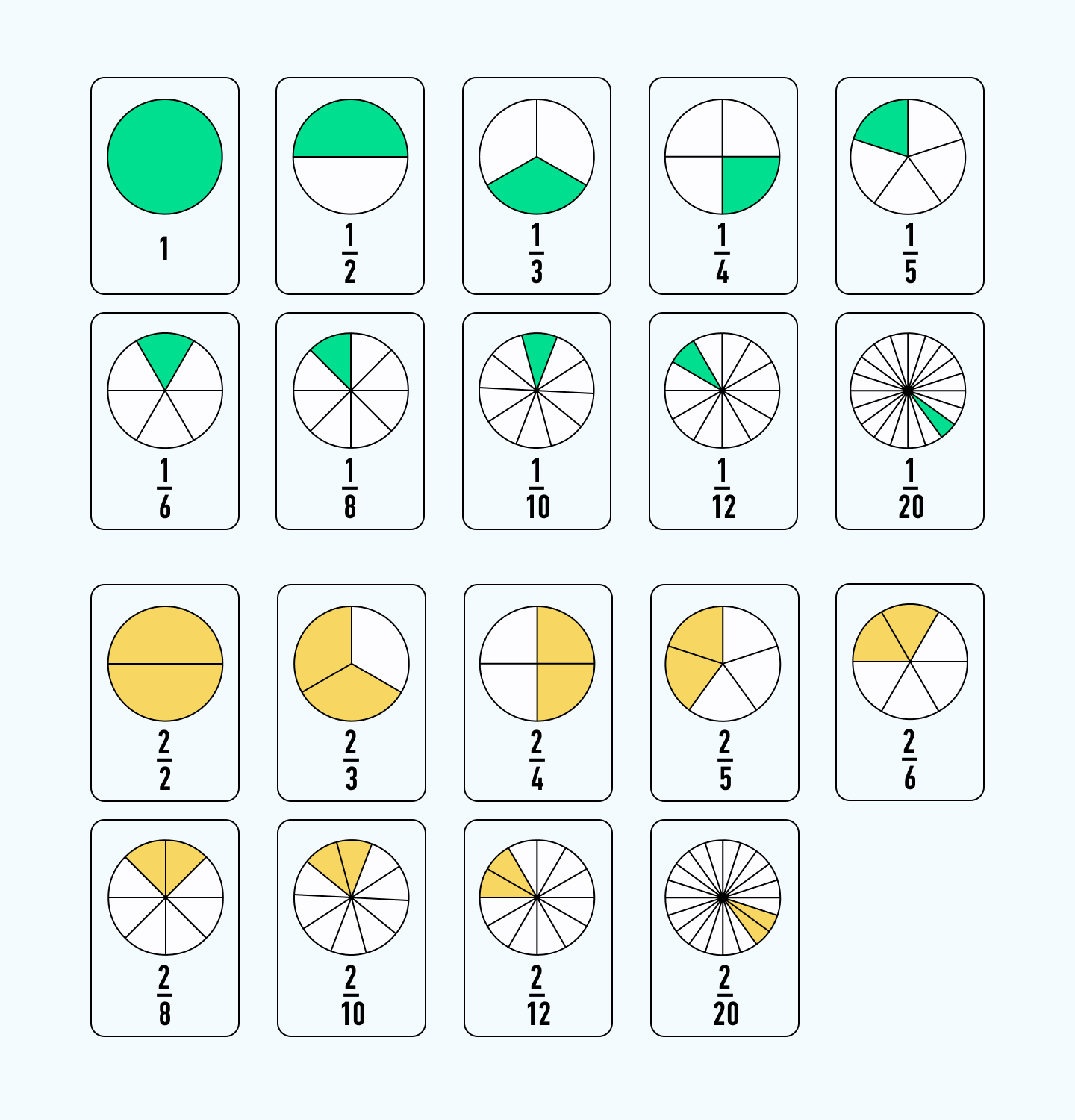
Рассмотрим обыкновенные дроби на примере отрезка или угла. Представим, что у нас есть отрезок, который разделен на 4 равные части. Каждая часть считается отдельной долей или обыкновенной дробью. В этом случае число 1 является целым числом, а каждая дробь, такая как 1/4, 2/4, 3/4 и 4/4, представляет собой обыкновенную дробь.

Чтобы записать обыкновенную дробь, используется две числа — числитель и знаменатель, разделенные чертой. Числитель — это число, которое располагается над чертой, а знаменатель — под чертой. Например, 1/4.

Для сравнения обыкновенных дробей нужно сравнивать числители и знаменатели. Так, например, дробь 1/4 меньше дроби 3/4. Чтобы найти общий знаменатель для разных дробей, нужно делить числитель одной дроби на знаменатель другой и умножать оба числа на полученное значение. Например, если нам нужен общий знаменатель для дробей 1/4 и 2/5, мы делаем следующие операции: 4 * 5 = 20 и 5 * 4 = 20. Таким образом, общий знаменатель для этих двух дробей будет 20.

В обратную сторону, чтобы найти числитель дроби после деления яблок, нужно понять, сколько частей возьмется при делении единичного яблока на знаменатель дроби. Например, если у нас есть дробь 3/4, то при делении одного яблока на 4 мы берем 3 части. Таким образом, дробь 3/4 означает, что мы берем 3 части из 4 возможных.

Обыкновенные дроби возникли в древних времена и были использованы для записи координат точек на плоскости. Египтяне в своих трудах по математике использовали обыкновенные дроби для сравнения разных долей.

Итак, обыкновенные дроби — это числа, записываемые в виде общей дроби, с числителем и знаменателем. Они являются частью чисел и помогают нам сравнивать и складывать разные доли.

Запись и чтение долей

Доли могут быть записаны в виде обыкновенных дробей, или в виде десятичных дробей, или в виде процентов. Наиболее распространенной формой записи долей является обыкновенная дробь.

Запись долей в виде обыкновенных дробей

Обыкновенная дробь обозначается через черту. Черта делит долю на числитель и знаменатель. Например, треть отрезка можно записать как 1/3. Пята отрезка можно записать как 1/5. Дробные значения долей могут быть записаны как смешанные числа, например, 2 3/4.

Для записи доли числитель будет всегда меньше знаменателя. Если числитель равен знаменателю, то доля равна 1 целой. Если числитель равен 0, то доля равна 0. Если знаменатель равен 0, то дробь не определена и не имеет значения.

Чтение долей

При чтении доли, числитель читается как «сколько», а знаменатель читается как «частей». Например, дробь 3/4 читается как «три четверти». Дробь 1/2 читается как «одна вторая» и т.д.

Доли могут быть сравнимы между собой. Если числитель одной доли меньше числителя другой, то первая доля меньше второй. Если знаменатель одной доли меньше знаменателя другой, то первая доля больше второй.

Урок 32 Бесплатно Доли. Обыкновенные дроби

Всегда при операции деления чего-либо, мы можем получить доли. Другими словами, дроби будут обозначать части общего целого.

Известно, что каждая четвёртая часть будет обозначаться дробью, в которой числитель равен 1, а знаменатель — 4. Например, если мы разделили час на 4 равных части, то каждая часть будет называться четвертая.

Во времена Древних Египтян было известно только деление на две части — половину и целое. Половина обозначалась так: один из двух равных кусочков.

В древних трудах известны записи, что они делили части на половины, третьи, четвертые, пятые части и так далее. Такие дроби похожи на наши дроби, только имеют немного другую запись и чтение числа.

Например, если взять один торт и разделить его на 5 одинаковых частей, то каждая часть будет называться пятая. Пятых частей будет 5, поэтому дробь, обозначающая такую часть, будет иметь вид 1/5.

Нужно отметить, что дробная черта, которая будет делять числитель и знаменатель, еще не была известна египтянам. В этой записи они просто писали числа рядом друг с другом.

Также стоит отметить, что в древних египетских записях дробь была записана в виде двух чисел, координат X и Y, разделенных точкой. Например, дробь 1/5 могла быть записана как 1.0. Однако, это обозначение отличается от нашего современного представления десятичной дроби.

Интересно, что в Древнем Египте было также известно деление на дроби, равные 3/5 или 4/5, которые имеют вид обыкновенной дроби, но со знаменателем, отличным от чисел, кратных пяти. Например, такая дробь делила расстояние между двумя точками на пять равных частей.

В сравнении с древними египетскими счислениями, обозначение и чтение десятичных дробей упростились. Теперь мы можем представить любое количество частей, например третью или десятую, используя десятичную запись. Например, 0.5 означает половину, а 0.1 — десятую часть.

Итак, в этом уроке мы познакомились с обыкновенными дробями, которые используются для обозначения частей общего целого. Мы узнали, что дробь представляет собой отрезок, разделенный на равные части. Числитель дроби указывает, сколько из этих частей мы взяли, а знаменатель указывает, на сколько частей разделен отрезок.

Что значит целая доля

Например, если у нас есть торт, который разделили на 4 равные части, то каждая часть будет обозначаться как одна четвертая доля или 1/4. Если каждая из этих частей тоже будет разделена на 3 равные части, то каждая из этих маленьких частей будет обозначаться как одна двенадцатая доля или 1/12.

Целая доля может быть любого вида, например, можно разделить объект на 5 равных частей и обозначить каждую часть как одну пятую долю или 1/5. Или можно разделить объект на 3 равных части и обозначить каждую часть как одну третью долю или 1/3.

Отношение между числителем и знаменателем определяет размер целой доли. Если числитель равен 1, то это означает, что у нас есть одна такая доля, а если числитель равен 2, то это означает, что у нас есть две таких доли.

Часто в уроках математики целые доли также называют обыкновенными дробями. В истории математики обыкновенные дроби были известны еще в древней Египте, где их использовали для счисления и измерения разных величин.

Обыкновенные дроби возникли еще во время возникновения десятичной системы счисления и служили для более точного измерения и записи разных размеров и количеств. С помощью обыкновенных дробей можно точно указать дробное значение и делить целые числа на части.

Действия с целыми долями аналогичны действиям с обыкновенными дробями. Они могут складываться, вычитаться, умножаться и делиться между собой. Для выполнения операций с целыми долями, их числители и знаменатели должны иметь одинаковые знаменатели. При выполнении операций результат может быть другой целой долей, дробью или целым числом.

Итак, целая доля представляет собой часть от целого числа, которую обычно обозначают в виде обыкновенной дроби. Она имеет числитель, обозначающий количество долей, и знаменатель, обозначающий количество одинаковых долей. Целые доли широко используются в математике для измерения и записи разных размеров и количеств.

Половина

В математике половину обозначают как $\frac{1}{2}$ или $0.5$.

Половина является самой простой формой дроби, которая представляет собой одну из равных частей целого числа или предмета.

Например, если у вас есть яблоко, то половина это ровно половина яблока, которая остается после того, как вы его разрезали пополам.

В древних времена, египтяне использовали половину как одну из основных долей для измерения и сравнения. Они называли половину «ведерку», которая записывалась как «½».

Половина также может быть выражена в виде десятичной дроби, где $0.5$ представляет половину целого числа.

Половина имеет свою особенность — она является одной из третьих долей. Например, если мы разделим целое число или предмет на три равные части, то каждая из этих частей будет равна $0.5$, или $\frac{1}{2}$.

Также можно сравнивать разные доли с половиной. Например, половина больше третьей доли, но меньше четвертой доли.

Половину можно использовать и для упрощения сложных математических операций. Например, чтобы найти половину числа, нужно разделить его на два.

Половина также находит применение в различных областях, таких как геометрия, где половина четырехугольника обозначается как «$\mathbf{\frac{1}{2}}$». Эта черта располагается над фигурой и указывает на долю, которая составляет половину от общего.

Изучение половин легко, и вы можете найти много примеров ее использования в повседневной жизни, в тестах, чтении и многих других трудах. Знание половины поможет вам лучше понять и использовать дроби в различных контекстах.

Сравнение долей

Чтобы сравнить доли, нужно сравнить их числительные или знаменатели. Если числительные одинаковые, значит доли равны. Если числитель одной доли больше, чем у другой, то эта доля больше. Например, если у нас есть доля 1/2 и доля 1/4, то 1/2 больше, потому что числитель у нее больше.

Сравнение долей может быть полезным в различных ситуациях. Например, если у нас есть 8 часов свободного времени и мы хотим сравнить, какую долю времени займет то или иное занятие. Если мы хотим провести 2 часа в библиотеке и 4 часа с друзьями, то сравнение долей поможет нам понять, сколько времени мы потратим на каждое из этих занятий.

Сравнение долей также может быть полезно при работе с геометрическими фигурами. Например, мы можем сравнить доли углов или доли расстояния на координатной оси.

Известно, что использование долей уходит своими корнями в древние времена. В древности египтяне использовали доли для счисления и выполнения различных действий с отрезками. Они называли долю, которая составляет одну часть отрезка из десяти частей, «десятью». Древние египтяне были не единственными, кто использовал доли. Другие древние народы, такие как древние греки и римляне, также использовали доли для записи дробных чисел и сравнения их.

Сравнение долей является важной математической операцией, и оно имеет много практических применений в нашей жизни. Например, оно может быть использовано для определения доли торта, которую можно съесть. Если у нас есть целая торт и мы хотим сравнить доли, которую каждый человек получит, то мы можем разделить торт на равные кусочки и сравнить их.

В итоге, сравнение долей помогает нам понять, какое количество чего-либо будет взято из целого. Благодаря доле, мы можем найти общую точку в разных виде действий и записей. Это позволяет нам проводить сравнение долей, чтобы найти целые и разделить их на равные кусочки.

Четверть

В дробной записи четверть обозначается символом ¼. Эта четверть называется четвертью доли и она располагается под чертой, а над ней написано число 4. Такая запись означает, что числитель равен 1, а знаменатель равен 4. Но можно иначе записать четверть, написав 1/4, где числитель и знаменатель отделяются чертой.

Четверть можно представить в виде графического изображения. Например, мы можем нарисовать круг и разделить его на 4 равные части. Одну из этих частей называем четвертю. Еще один способ представления — это изображение линии, разделенной на 4 равные отрезки. Одним из таких отрезков является четверть.

В истории дробей четверть была известна еще в древние времена. Например, египтяне в своем счислении использовали только обыкновенные дроби. Для них 1/4 это одна четвертая, которую они обозначали чертой, расположенной над числом 4. Примеры использования четверти есть не только в математических задачах. Например, если мы взяли целый торт и разделили его на 4 равные части, то каждая часть будет называться четвертью. Аналогично, если у нас есть час и мы разделили его на 4 равные участка, то каждый участок будет называться четвертью часа, а общее количество четвертей — 4.

Часто в жизни мы сталкиваемся с ситуацией, когда нужно выполнять действия с четвертью. Например, если у нас есть общая длина отрезка и нам нужно разделить его на 4 равные части, то каждая часть будет называться четвертью этой длины. Если мы имеем круг и нам нужно найти площадь четверти этого круга, то мы должны разделить площадь круга на 4.

Примеры использования четверти:

1. Я съел только четверть яблока.

2. Четверть часа равна 15 минутам.

Треть

История возникновения понятия «треть» уходит в древние времена. Египтяне, например, уже знали и использовали эту долю в своих трудах. Они разделяли одно целое на три равные части и называли каждую часть «третью».

Треть обозначается числом 1 снизу и цифрой 3 сверху, справа от числа. Такая запись выглядит как:

1

—

3

Чтение этой записи осуществляется следующим образом: «1 треть».

Треть часто встречается в нашей повседневной жизни. Например, чтобы поделить пирог на три равные части, нужно разрезать его на три одинаковых отрезка. Точка, где будет производиться разрез, будет располагаться на расстоянии одной трети от начала теста. Также треть может быть использована для разделения времени: если день состоит из 24 часов, то одна треть дня будет составлять 8 часов.

Помимо трети, существуют и другие доли, такие как половина (1/2), четверть (1/4), пятая (1/5) и т.д. Чтобы сравнить различные доли, можно использовать общий знаменатель. Например, треть и четверть можно сравнить, если использовать знаменатель, равный 12. Такая частота деления позволяет найти эквивалентные доли и сравнить их.

Третью долю можно записать и как десятичную дробь, например 0.33(3), где тройка повторяется бесконечно. Такое представление числа более удобно для вычислений и решения математических задач.

Третий тест будет следующим: чтобы сравнить треть и четверть, мы будем использовать общий знаменатель, равный 12. Вначале запишем треть в виде обыкновенной дроби:

4

—

12