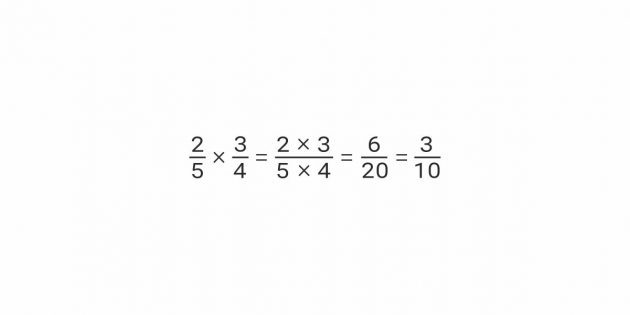Что такое умножение дробей и как правильно выполнять эту операцию

Умножение дробей — это одно из основных действий в арифметике, поэтому важно понять его правила и научиться выполнять. Дроби представляют собой числа, которые записываются в виде одной дроби или смешанной дроби. Видео в конце статьи дадим практическое решение задач на умножение дробей и научимся выполнить это действие корректно и без ошибок.

Умножение дробей происходит по правилу: числитель первой дроби умножается на числитель второй дроби, а затем делитель первой дроби умножается на делитель второй дроби. После этого полученное произведение числителей и делителей записывается в виде новой дроби. Чтобы найти значение этой дроби в виде натурального числа, необходимо выполнить дополнительные действия, облегчающие решение задач.

Например, если умножить две обыкновенные дроби, такие как 2/3 и 3/4, то сначала числитель первой дроби умножается на числитель второй дроби: 2 * 3 = 6. Затем делитель первой дроби умножается на делитель второй дроби: 3 * 4 = 12. Полученное произведение 6/12 может быть упрощено путем сокращения числителя и делителя на их общий делитель. В данном случае общим делителем является число 6, поэтому упрощенное значение дроби будет 1/2.

Смешанные числа также можно умножать. Смешанная дробь состоит из целой части и дробной части, разделенных чертой. Чтобы выполнить умножение смешанной дроби на целое число или другую дробь, сначала нужно превратить смешанную дробь в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и прибавить числитель к произведению. Затем получившаяся неправильная дробь умножается как обычные обыкновенные дроби.

Вся теория умножения дробей и примеры выполнения этого действия представлены в видео ниже. Посмотрите видео и прокачайте свои навыки в умножении дробей!

Умножение дробей

Чтобы понять, что такое умножение дробей и как его выполнять, рассмотрим следующую задачу.

Задача:

Найдите произведение двух дробей: 2/3 и 4/5.

Для решения этой задачи существуют правила умножения дробей. Давайте их рассмотрим.

Правила умножения дробей:

1. Числитель полученной дроби равен произведению числителей этих дробей.

2. Знаменатель полученной дроби равен произведению знаменателей этих дробей.

Теперь применим эти правила к нашей задаче:

Числитель полученной дроби равен 2 * 4 = 8.

Знаменатель полученной дроби равен 3 * 5 = 15.

Значит, произведение дробей 2/3 и 4/5 равно 8/15.

Однако, в некоторых задачах может быть дана необратная дробь или дробь в виде смешанного числа. В таком случае нужно перевести дроби к обыкновенному виду и затем умножить.

Например, произведение дробей 2 1/7 и 3/4:

Сначала переведем смешанную дробь 2 1/7 в обыкновенную:

2 1/7 = (2 * 7 + 1) / 7 = 15/7.

Теперь умножим полученную дробь 15/7 на 3/4:

Числитель полученной дроби равен 15 * 3 = 45.

Знаменатель полученной дроби равен 7 * 4 = 28.

Значит, произведение дробей 2 1/7 и 3/4 равно 45/28.

Также, при умножении дробей можно сокращать числитель и знаменатель на их общие делители, чтобы получить простую дробь.

Например, произведение дробей 415/556 и 217/3:

Давайте найдем общий делитель чисел 415 и 556:

415 = 5 * 83,

556 = 2 * 2 * 139.

Общих делителей у этих чисел нет, значит, дробь 415/556 не может быть сокращена.

Но затем мы можем сократить дробь 217/3:

217 = 7 * 31,

3 = 3 * 1.

Таким образом, произведение дробей 415/556 и 217/3 равно (415 * 7) / (556 * 1) = 2905/556.

Также, стоит отметить, что при умножении дробей результат может быть равен нулю, если одна из дробей равна нулю или числитель одной из дробей равен нулю.

Нахождение обратной дроби:

Обратная дробь — это дробь, при умножении которой на исходную дробь получается целое число равное единице.

Например, обратной к дроби 3/4 является дробь 4/3.

Также существует правило нахождения обратной дроби:

Для нахождения обратной дроби, нужно заменить числитель и знаменатель местами.

Заключение

Таким образом, умножение дробей — это процесс, при котором произведение числителей дробей становится новым числителем, а произведение знаменателей — новым знаменателем.

Правила умножения дробей позволяют найти произведение любых дробей, включая дроби в обыкновенном и смешанном виде.

Также, сокращение дроби и нахождение обратной дроби облегчает решение задач, связанных с умножением дробей.

Умножение дробей: теория и практика

Теория

Дробь представляет собой математическое выражение в виде одного числа, разделенного на другое числом чертой. Например, дробь 2/3 состоит из числителя 2 и знаменателя 3.

Обыкновенные дроби и смешанные числа также могут быть представлены в виде дробей. Смешанная дробь представляет собой сумму целой части и обыкновенной дроби. Например, число 4 2/5 может быть записано в виде дроби 22/5.

Умножение дробей происходит путем перемножения числителей и знаменателей. Полученное произведение числителей становится новым числителем, а произведение знаменателей — новым знаменателем.

Если одна из дробей имеет числитель, равный нулю, то результат умножения будет равен нулю.

Практика

Давайте решим пример по умножению дробей:

1. Задача: Выполнить умножение дробей 2/3 и 4/5.
2. Задание: Найти произведение числителей и знаменателей дробей.
3. Действие: Умножить числители: 2 * 4 = 8, умножить знаменатели: 3 * 5 = 15.
4. Решение: Полученная дробь равна 8/15.

Таким образом, умножение дробей 2/3 и 4/5 равно 8/15.

Для облегчения решения задач по умножению дробей рекомендуется сокращать знаменатели до натуральных чисел. Для этого необходимо найти общий делитель чисел, которые составляют знаменатели дробей, и затем разделить каждое число на этот общий делитель.

Также стоит отметить, что умножение дробей является взаимно обратной операцией по отношению к сложению. Это значит, что если мы умножаем дроби в одной задаче, то можем получить эти же дроби, если выполним сложение в другой задаче.

Правило умножения дробей

Как мы уже знаем, дробь состоит из двух частей: числителя и знаменателя. Правило умножения дробей гласит, что чтобы умножить две обыкновенные дроби, нужно умножить их числители и затем знаменатели. Такое действие также выполняется при умножении смешанных чисел: сначала нужно умножить целую часть на числитель дроби, а затем прибавить полученное произведение к числителю.

Давайте рассмотрим пример. Задание: найти произведение дроби 2/3 и дроби 5/6.

Шаг 1: Умножаем числители 2 и 5: 2 * 5 = 10.

Шаг 2: Умножаем знаменатели 3 и 6: 3 * 6 = 18.

Полученное произведение числителей и знаменателей равно 10/18.

Шаг 3: Сокращаем знаменатель 18, получаем 10/9 в простейшем виде.

Ответ: произведение дроби 2/3 и дроби 5/6 равно 10/9.

Важно знать, что при умножении дроби на целое число результатом будет дробь, которая имеет тот же знаменатель, а числитель будет равен произведению числителя дроби на целое число.

Например, если нужно умножить дробь 3/4 на целое число 5, то результат будет равен 3 * 5 = 15/4.

Знание правила умножения дробей позволит легко решать задачи, связанные с определением произведения дробей и целых чисел.

Как умножить дробь на натуральное число

Если нужно умножить дробь на натуральное число, то числитель дроби умножается на это число, а знаменатель остается прежним.

Например, для умножения дроби 2/3 на число 4 мы должны умножить числитель 2 на 4, что даст нам 8, и оставить знаменатель равным 3. Таким образом, результатом умножения будет дробь 8/3.

Если у нас есть смешанная дробь, которая состоит из целой части и дробной части, то сначала нужно превратить ее в неправильную дробь. Для этого мы умножаем целую часть на знаменатель и прибавляем числитель к этому произведению. Затем умножаем полученное число на вторую дробь так же, как мы это делали ранее.

Например, если у нас есть смешанная дробь 2 1/4, мы должны сначала превратить ее в неправильную дробь. Для этого умножаем 2 на 4 и добавляем 1 к этому произведению. Получаем результат 9/4. Затем умножаем эту дробь на третью дробь по тому же принципу, как и в предыдущем примере.

Правила умножения дробей являются взаимно обратными правилам деления дробей. То есть, чтобы умножить дробь на число, мы можем сначала изменить эту дробь на обратную и затем выполнить деление на это число.

Видео о теории обыкновенных дробей, сокращении и умножении:

Также давайте рассмотрим несколько практических задач:

Задача 1:

Что получится, если умножить дробь 3/4 на число 5?

Решение:

Умножаем числитель 3 на 5 и оставляем знаменатель без изменений. Получаем дробь 15/4.

Задача 2:

Чему равно произведение дроби 2 3/5 на число 2?

Решение:

Превращаем смешанную дробь 2 3/5 в неправильную дробь. Умножаем целую часть 2 на знаменатель 5 и прибавляем числитель 3. Получаем дробь 13/5. Умножаем эту дробь на число 2, умножая числитель 13 на 2 и оставляя знаменатель равным 5. Результатом умножения будет дробь 26/5.

Таким образом, умножение дробей на натуральное число – это простое действие, которое не требует особых математических навыков. Главное – понять правила и их применение в практике задач.

Умножение обыкновенных дробей

Для умножения дробей нужно сначала умножить числители между собой, а затем знаменатели. При этом правило нахождения произведения чисел относительно сложения остается прежним. Если числители дробей являются смешанными числами, то сначала их приводят к неправильной дроби.

Рассмотрим примеры:

Пример 1:

Найти произведение дробей 2/3 и 1/4.

Для решения этой задачи мы сначала умножим числители между собой: 2 * 1 = 2. Затем умножим знаменатели: 3 * 4 = 12. Полученное произведение числителя и знаменателя составит ответ на задачу: 2/3 * 1/4 = 2/12 = 1/6.

Пример 2:

Найти произведение смешанных чисел 2 1/4 и 3 2/7.

Для решения этой задачи мы сначала приведем смешанные числа к неправильным дробям: 2 1/4 = (2 * 4 + 1) / 4 = 9/4 и 3 2/7 = (3 * 7 + 2) / 7 = 23/7. Затем умножим полученные дроби между собой: (9/4) * (23/7) = 207/28.

Таким образом, умножение обыкновенных дробей происходит путем умножения числителей и знаменателей, а при необходимости приведения смешанных чисел к неправильным дробям.

Как умножить дробь на дробь

Правило умножения дробей

Для умножения двух дробей сначала перемножаем числители, а затем делаем то же самое с знаменателями. Полученные два произведения числителей и знаменателей являются числителем и знаменателем произведения этих двух дробей соответственно.

На примере:

Умножим дробь 2/3 на дробь 1/6.

Перемножим числители: 2 * 1 = 2.

Перемножим знаменатели: 3 * 6 = 18.

Таким образом, произведение дробей 2/3 и 1/6 равно 2/18, что в свою очередь можно сократить до 1/9.

Умножение дроби на целое число

Умножение дроби на целое число также выполняется по тому же правилу. Числитель дроби умножается на целое число, а знаменатель остается прежним.

На примере:

Умножим дробь 3/4 на целое число 5.

3 * 5 = 15.

Таким образом, произведение дроби 3/4 и целого числа 5 равно 15/4.

Умножение смешанных чисел

Для выполнения умножения смешанных чисел необходимо следовать определенным правилам. Давайте рассмотрим эти правила на конкретном примере.

Пример: Найдите произведение чисел 217 и 415.

Решение задачи:

1. Первым шагом необходимо записать смешанную дробь в виде неправильной дроби. Для этого умножим целую часть на знаменатель и прибавим числитель. В примере 217 это 2 * 7 + 1 = 15.
2. После этого произведение двух смешанных чисел записывается в виде произведения их числителей и знаменателей. В нашем случае это 15/7 * 415/1.
3. Далее произведение числителей и знаменателей выполняется как обычное умножение дробей. Умножим числители: 15 * 415 = 6225. И умножим знаменатели: 7 * 1 = 7.
4. Полученное произведение записывается в виде дроби: 6225/7.
5. Чтобы найти ответ, необходимо записать дробь 6225/7 в виде смешанной дроби: целая часть равна результату деления числителя на знаменатель (6225/7 = 889 остаток 2).
6. Ответ: произведение чисел 217 и 415 равно 889 2/7.

Таким образом, умножение смешанных чисел находится путем выполнения нескольких действий, которые включают перевод в вид неправильной дроби, умножение числителей и знаменателей, а затем запись ответа в виде смешанной дроби. Это понятие существует относительно всех чисел и может быть решено с помощью правила умножения дробей.

Основные правила умножения смешанных чисел:

1. Умножайте целую часть на знаменатель и прибавляйте числитель.
2. Верными числами по отношению к знаменателям являются смешанные числа.
3. Умножение дробей выполняется умножением числителей и знаменателей.
4. Результатом умножения смешанных чисел будет смешанное число.

Подводя итог, умножение смешанных чисел состоит из нескольких действий, которые выполняются в определенном порядке. Правильное выполнение этих действий позволяет найти произведение двух смешанных чисел. Знание основных правил умножения смешанных чисел позволяет легко решать задачи с использованием этой операции.

Как умножить смешанные дроби Для понимания и выполнения этого умножения, давайте разберемся с понятием смешанной дроби. Смешанная дробь состоит из целой части и обыкновенной дроби, объединенных чертой, например, 3 1/2. Видео 1. Как умножать смешанные дроби. Основные правила умножения смешанных дробей: Разделяем целую часть и обыкновенную дробь с помощью пробела. Производим умножение между целыми числами и обыкновенными дробями отдельно. Потом складываем полученные произведения целых чисел и обыкновенных дробей. Сокращаем полученную смешанную дробь, если это возможно. Попробуем выполнить задание на примере. Дано: 5 1/2 * 3 2/3. 1. Разделим целую часть и обыкновенную дробь: 5 1/2 × 3 2/3 2. Выполняем умножение между целыми числами и обыкновенными дробями отдельно: 5 × 3 15 1/2 × 2/3 1/3 3. Складываем полученные произведения целых чисел и обыкновенных дробей: 15 + 1/3 15 1/3 4. Полученное произведение 15 1/3 является итоговым ответом. Также стоит отметить, что смешанные числа можно представить в виде обыкновенной дроби, и после получения ответа можно привести его к смешанной дроби при необходимости. Умножение смешанных дробей – это практическое применение теории, которая облегчает понимание и выполнение задач нахождения произведения между смешанными числами. Практика и понимание правил помогут успешно решать подобные задачи.

Видео:

УМНОЖЕНИЕ ДРОБЕЙ с разными знаменателями 5 6 класс

УМНОЖЕНИЕ ДРОБЕЙ с разными знаменателями 5 6 класс by физика ОГЭ математика ЕГЭ — Романов Владимир 108,636 views 6 years ago 2 minutes, 15 seconds